Generalization bounds with arbitrary complexity measures

Résumé

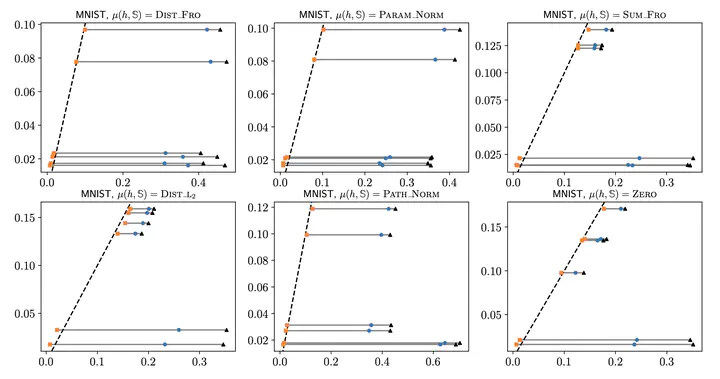
In statistical learning theory, a generalization bound usually involves a complexity measure imposed by the considered theoretical framework. This limits the scope of such bounds, as other forms of capacity measures or regularizations are used in algorithms. In this paper, we leverage the framework of disintegrated PAC-Bayes bounds to derive a general generalization bound instantiable with complexity measures. One trick to prove such a result is to consider a commonly used family of distributions: the Gibbs distributions. Our bound stands in probability jointly over the hypotheses and the learning sample, which allows the complexity to be adapted to the generalization gap as it can be customized to fit both the hypothesis class and the task.