Fast Convergence of Softmax Policy Mirror Ascent

Résumé

We analyze the convergence of a novel policy gradient algorithm (referred to as SPMA) for multi-armed bandits and tabular Markov decision processes (MDPs). SPMA is an instantiation of mirror ascent and uses the softmax parameterization with a log-sum-exp mirror map. Given access to the exact policy gradients, we prove that SPMA with a constant step-size requires iterations to converge to an -optimal policy. The resulting convergence rate is better than both the

rate for constant step-size softmax policy gradient (SPG) and the

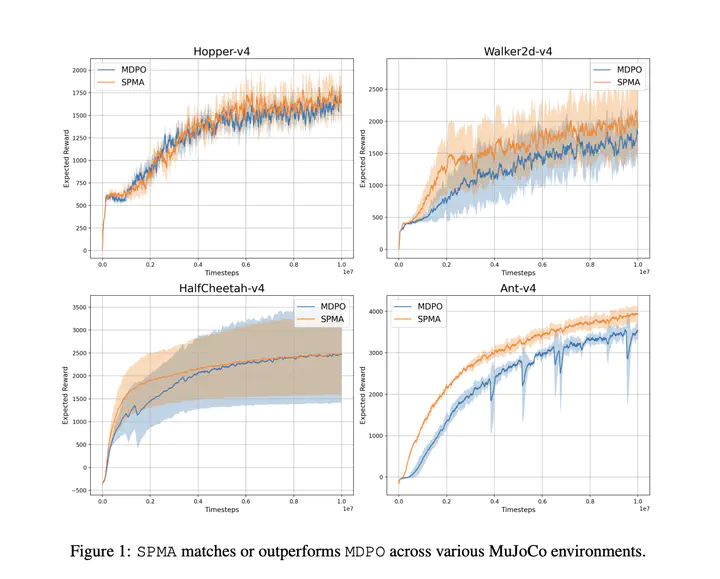
rate for SPG with Nesterov acceleration. Furthermore, unlike the SPG results, the convergence rate for SPMA does not depend on potentially large problem-dependent constants, and matches the rate achieved by natural policy gradient (NPG). Furthermore, for multi-armed bandits, we prove that SPMA with gap-dependent step-sizes can result in global super-linear convergence. Our experimental evaluations on tabular MDPs and continuous control tasks demonstrate that SPMA consistently outperforms SPG while achieving similar or better performance compared to NPG.