Sample compression unleashed: New generalization bounds for real valued losses

Abstract

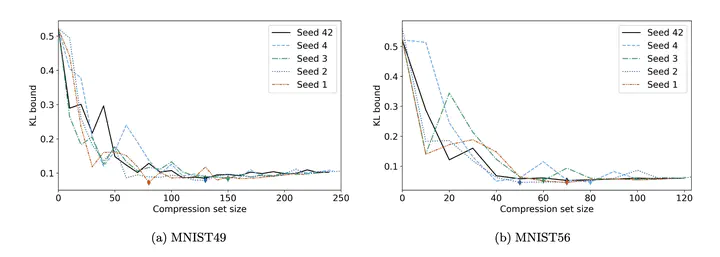
The sample compression theory provides generalization guarantees for predictors that can be fully defined using a subset of the training dataset and a (short) message string, generally defined as a binary sequence. Previous works provided generalization bounds for the zero-one loss, which is restrictive notably when applied to deep learning approaches. In this paper, we present a general framework for deriving new sample compression bounds that hold for real-valued unbounded losses. Using the Pick-To-Learn (P2L) meta-algorithm, which transforms the training method of any machine-learning predictor to yield sample-compressed predictors, we empirically demonstrate the tightness of the bounds and their versatility by evaluating them on random forests and multiple types of neural networks.