Surrogate Minimization: An Optimization Algorithm for Training Large Neural Networks with Model Parallelism

Abstract

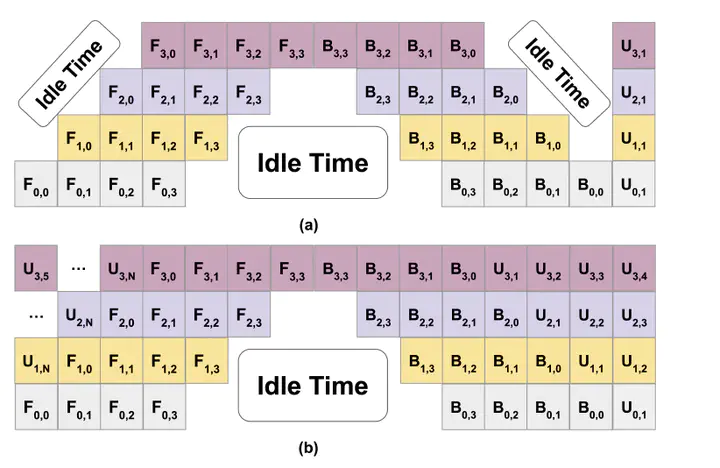
Optimizing large memory-intensive neural networks requires distributing its layers across multiple GPUs (referred to as model parallelism). We develop a framework that allows decomposing a neural network layer-wise and training it by optimizing layer-wise local losses in parallel. By using the resulting framework with GPipe [12], an effective pipelining strategy for model parallelism, we propose the Surrogate Minimization (SM) algorithm. SM allows for multiple parallel updates to the layer-wise parameters of a distributed neural network and consequently improves the GPU utilization of GPipe. Our framework ensures that the sum of local losses is a global upper-bound on the neural network loss, and can be minimized efficiently. Under mild technical assumptions, we prove that SM requires O(1/ϵ) iterations in order to guarantee convergence to an ϵ-neighbourhood of a stationary point of the neural network loss. Finally, our experimental results on MLPs demonstrate that SM leads to faster convergence compared to competitive baselines.