Generalization Bounds via Meta-Learned Model Representations: PAC-Bayes and Sample Compression Hypernetworks

Abstract

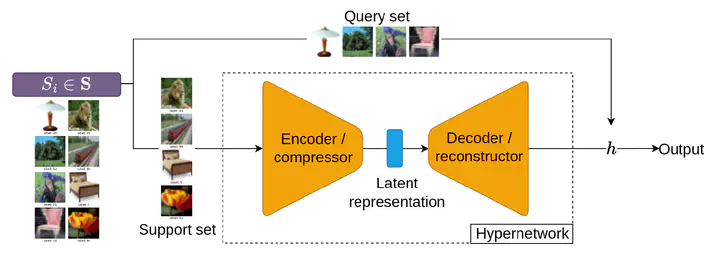
Both PAC-Bayesian and Sample Compress learning frameworks have been shown instrumental for deriving tight (non-vacuous) generalization bounds for neural networks. We leverage these results in a meta-learning scheme, relying on a hypernetwork that outputs the parameters of a downstream predictor from a dataset input. The originality of our approach lies in the investigated hypernetwork architectures that encode the dataset before decoding the parameters: (1) a PAC-Bayesian encoder that expresses a posterior distribution over a latent space, (2) a Sample Compress encoder that selects a small sample of the dataset input along with a message from a discrete set, and (3) a hybrid between both approaches motivated by a new Sample Compress theorem handling continuous messages. The latter theorem exploits the pivotal information transiting at the encoder-decoder junction in order to compute generalization guarantees for each downstream predictor obtained by our meta-learning scheme.